We created a series of three tasks that can be implemented in Abstract Algebra courses to help students in their understanding of the course material and foster collaboration among students as they engage in meaningful ways with key ideas and proofs.
Curricular Materials
High Leverage Teaching Practices
In order to support students in this meaningful mathematical activity, we identified and adapted a set of high leverage teaching practices (HLTP) studied in K-12 classrooms to the advanced proof-based setting (undergraduate classes where formal proofs are one of the primary objects of study). These practices are “routine aspects of teaching, which guide teachers to integrate students’ thinking, content knowledge, and equity” (Woods & Wilhelm, 2020, p. 106).
In general, we found that HLTPs translated well to the proof setting, but required increased attention to navigating between formal and informal mathematics, developing precision around mathematical objects, supporting competencies beyond formal proof construction, and structuring group work. Below are the four main HLTPs we focused on in our development of these tasks.
Launching Complex Tasks
The teacher engages students in making sense of tasks via attending to relevant mathematical language, ideas, relationships, task contextual features, and development of a common understanding of the task goals and context. This practice occurs prior to or in parallel with problem-solving, but does not scaffold or directly instruct on solutions to the task.
Structuring Group and Partner Work
The teacher structures and manages partner and group work in order to engage all students meaningfully in mathematical activity. This can include scripts, clear mathematical activity expectations, and/or roles that provide guidance for how students are to interact with each other and the mathematics.
Selecting and Working with Public Records of Student Ideas
The teacher orchestrates mathematical discussion where (1) students publicly present ideas and (2) students are prompted to meaningfully engage with the ideas through analyzing, critiquing, and/or comparing across student ideas.
Using and Connecting Representations
The teacher introduces (or supports students in introducing) visual representations that encode mathematical meaning or structure in order to support students in engaging, communicating, or making sense of a mathematical idea or scenario. The teacher encourages connections between representations (visual, verbal, symbolic) and promotes connections to mathematically normative language.
Task 1: Structural Property Proof
Task 1 is meant to provide students an opportunity to analyze, compare, and correct two proofs of the statement, Suppose G and H are isomorphic groups. Then if G is abelian, H is abelian. — a structural property proof. By providing two previously constructed proof attempts of this statement, each partner in student pairs is given the task of becoming an ‘expert’ of a proof without the requirement of constructing the argument itself.
Students then engage in comparing and contrasting the two proofs, encouraging discussions regarding the assumptions necessary for the argument and the unpacking of related definitions, ultimately resulting in modified statements and proofs.
Task 2: Lagrange's Theorem
Task 2 is meant to help students to engage in the construction of a proof that involves diagrammatic reasoning and the development and use of lemmas to prove a larger result, namely Lagrange’s Theorem.
In this task, students use diagrammatic reasoning to see the multiplicative structure in cosets and explore examples to identify and generalize properties about cosets, formalize these statements, prove these lemma statements are true, and eventually construct a proof of Lagrange’s Theorem.
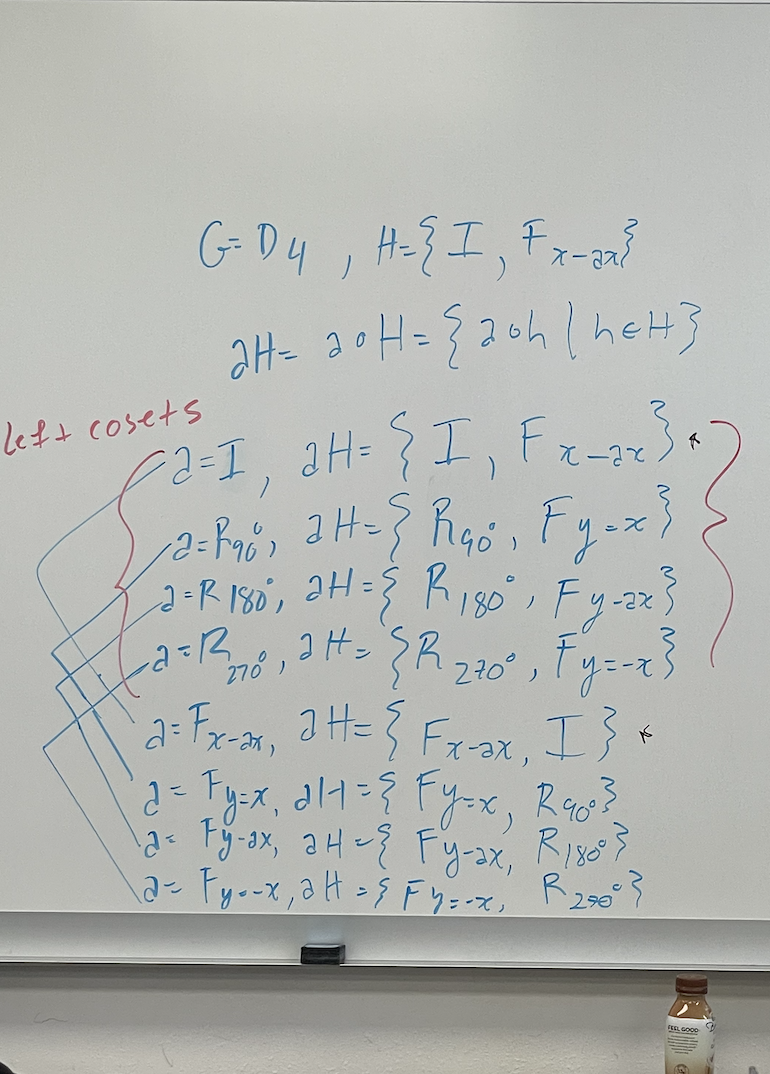
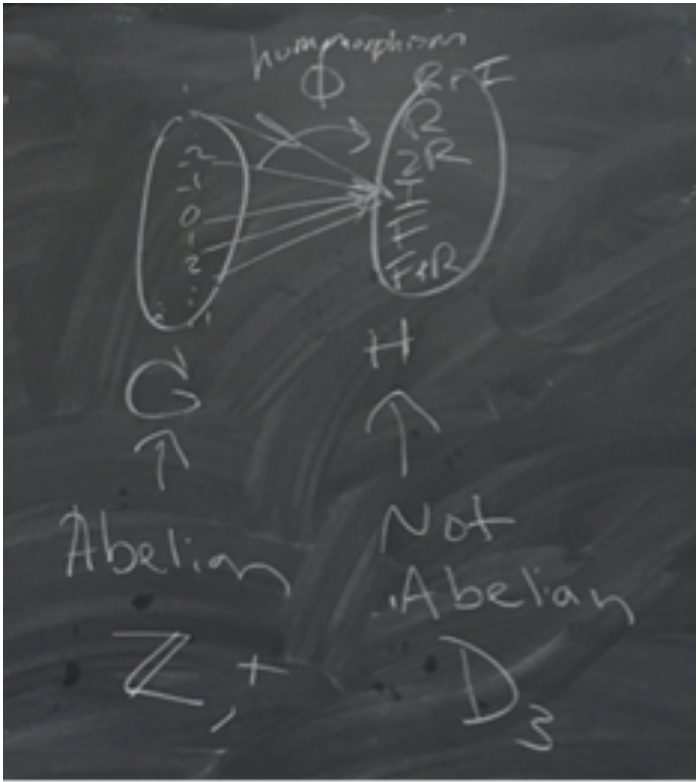
Task 3: Fundamental Homomorphism Theorem
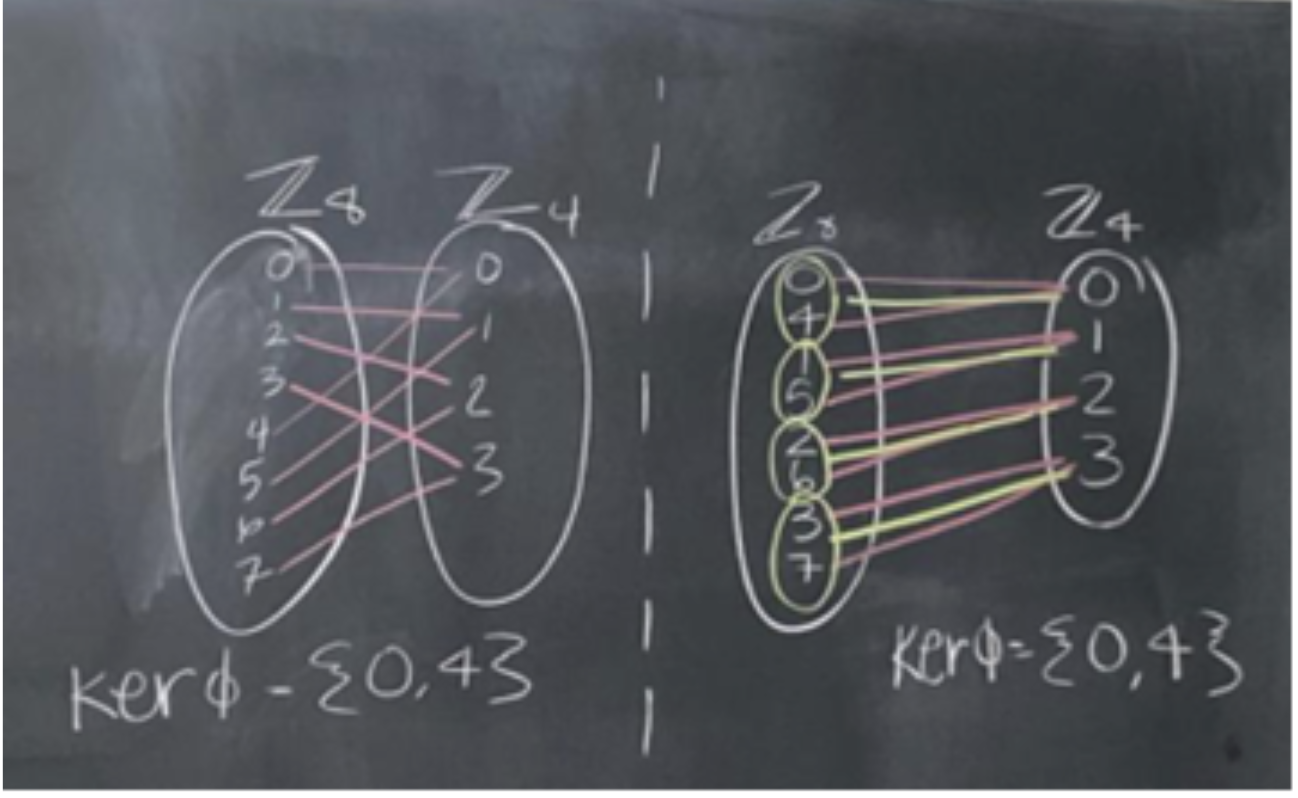
Task 3 is meant to help and support students in comprehending the First Isomorphism Theorem (or Fundamental Homomorphism Theorem) -- typically one of the more complex and final theorems discussed in an undergraduate abstract algebra course. The FIT contains multiple aspects of what students learn in an abstract algebra course. Normal groups, isomorphisms, homomorphisms, and quotient groups.
Further, students are typically shown the proof and not assigned to prove the theorem due to its complexity, as such this is the perfect theorem to help students explore the proof to comprehend its many parts. The goal of this activity is to give students the opportunity to work together in comprehending the Fundamental Isomorphism Theorem.
Would you like access to these materials?
Fill out the following form to request access!